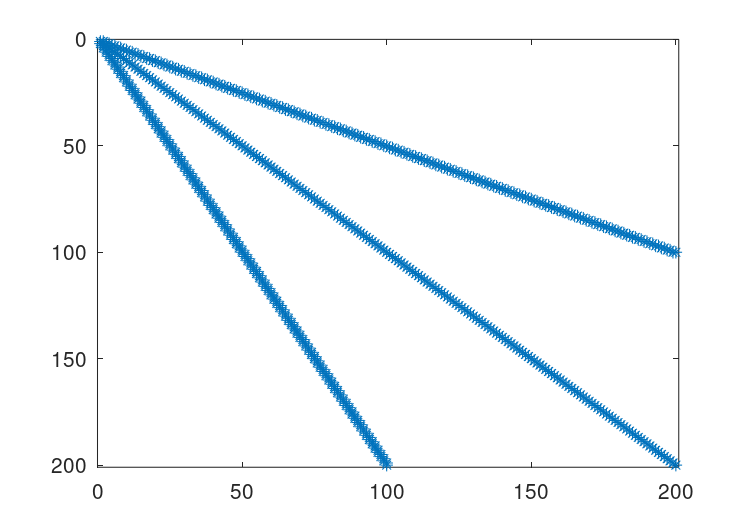
Figure 22.3: Structure of simple sparse matrix.
Previous: Return Types of Operators and Functions, Up: Operators and Functions [Contents][Index]
The attempt has been made to make sparse matrices behave in exactly the same manner as there full counterparts. However, there are certain differences and especially differences with other products sparse implementations.
First, the "./" and ".^" operators must be used with care.
Consider what the examples
s = speye (4); a1 = s .^ 2; a2 = s .^ s; a3 = s .^ -2; a4 = s ./ 2; a5 = 2 ./ s; a6 = s ./ s;
will give. The first example of s raised to the power of 2 causes
no problems. However s raised element-wise to itself involves a
large number of terms 0 .^ 0 which is 1. There s .^
s is a full matrix.
Likewise s .^ -2 involves terms like 0 .^ -2 which
is infinity, and so s .^ -2 is equally a full matrix.
For the "./" operator s ./ 2 has no problems, but
2 ./ s involves a large number of infinity terms as well
and is equally a full matrix. The case of s ./ s
involves terms like 0 ./ 0 which is a NaN and so this
is equally a full matrix with the zero elements of s filled with
NaN values.
The above behavior is consistent with full matrices, but is not consistent with sparse implementations in other products.
A particular problem of sparse matrices comes about due to the fact that as the zeros are not stored, the sign-bit of these zeros is equally not stored. In certain cases the sign-bit of zero is important. For example:
a = 0 ./ [-1, 1; 1, -1];
b = 1 ./ a
⇒ -Inf Inf
Inf -Inf
c = 1 ./ sparse (a)
⇒ Inf Inf
Inf Inf
To correct this behavior would mean that zero elements with a negative sign-bit would need to be stored in the matrix to ensure that their sign-bit was respected. This is not done at this time, for reasons of efficiency, and so the user is warned that calculations where the sign-bit of zero is important must not be done using sparse matrices.
In general any function or operator used on a sparse matrix will
result in a sparse matrix with the same or a larger number of nonzero
elements than the original matrix. This is particularly true for the
important case of sparse matrix factorizations. The usual way to
address this is to reorder the matrix, such that its factorization is
sparser than the factorization of the original matrix. That is the
factorization of L * U = P * S * Q has sparser terms L
and U than the equivalent factorization L * U = S.
Several functions are available to reorder depending on the type of the matrix to be factorized. If the matrix is symmetric positive-definite, then symamd or csymamd should be used. Otherwise amd, colamd or ccolamd should be used. For completeness the reordering functions colperm and randperm are also available.
See Figure 22.3, for an example of the structure of a simple positive definite matrix.

Figure 22.3: Structure of simple sparse matrix.
The standard Cholesky factorization of this matrix can be
obtained by the same command that would be used for a full
matrix. This can be visualized with the command
r = chol (A); spy (r);.
See Figure 22.4.
The original matrix had
598
nonzero terms, while this Cholesky factorization has
10200,
with only half of the symmetric matrix being stored. This
is a significant level of fill in, and although not an issue
for such a small test case, can represents a large overhead
in working with other sparse matrices.
The appropriate sparsity preserving permutation of the original
matrix is given by symamd and the factorization using this
reordering can be visualized using the command q = symamd (A);
r = chol (A(q,q)); spy (r). This gives
399
nonzero terms which is a significant improvement.
The Cholesky factorization itself can be used to determine the
appropriate sparsity preserving reordering of the matrix during the
factorization, In that case this might be obtained with three return
arguments as [r, p, q] = chol (A); spy (r).
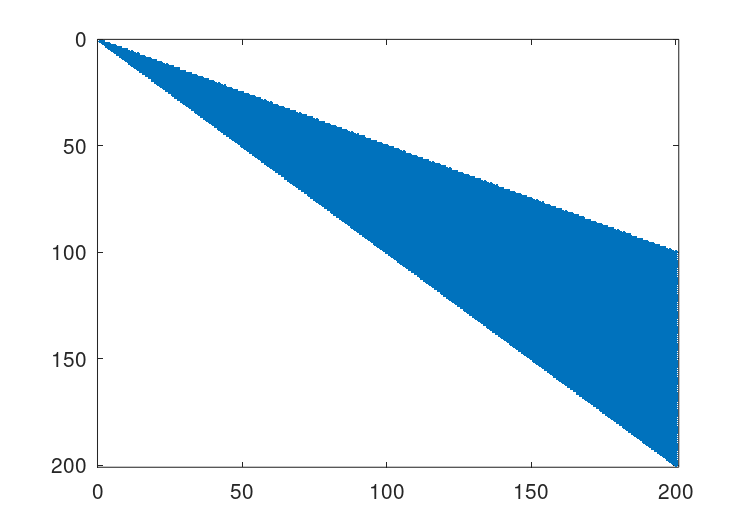
Figure 22.4: Structure of the unpermuted Cholesky factorization of the above matrix.
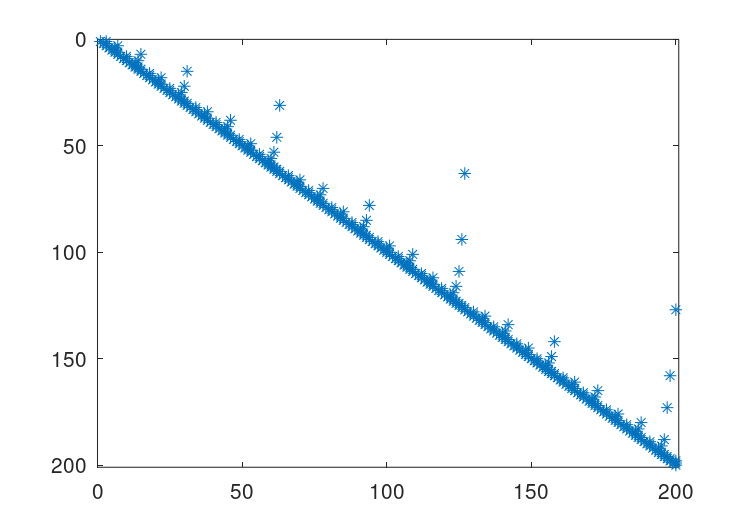
Figure 22.5: Structure of the permuted Cholesky factorization of the above matrix.
In the case of an asymmetric matrix, the appropriate sparsity
preserving permutation is colamd and the factorization using
this reordering can be visualized using the command
q = colamd (A); [l, u, p] = lu (A(:,q)); spy (l+u).
Finally, Octave implicitly reorders the matrix when using the div (/) and ldiv (\) operators, and so no the user does not need to explicitly reorder the matrix to maximize performance.
Return the approximate minimum degree permutation of a matrix.
This is a permutation such that the Cholesky factorization of
S (p, p) tends to be sparser than the
Cholesky factorization of S itself. amd is typically
faster than symamd but serves a similar purpose.
The optional parameter opts is a structure that controls the behavior
of amd. The fields of the structure are
Determines what amd considers to be a dense row or column of the
input matrix. Rows or columns with more than max (16, (dense *
sqrt (n))) entries, where n is the order of the matrix S,
are ignored by amd during the calculation of the permutation.
The value of dense must be a positive scalar and the default value is 10.0
If this value is a nonzero scalar, then amd performs aggressive
absorption. The default is not to perform aggressive absorption.
The author of the code itself is Timothy A. Davis (see http://faculty.cse.tamu.edu/davis/suitesparse.html).
Constrained column approximate minimum degree permutation.
p = ccolamd (S) returns the column approximate minimum
degree permutation vector for the sparse matrix S. For a
non-symmetric matrix S, S(:, p) tends to have
sparser LU factors than S.
chol (S(:, p)' * S(:, p)) also tends to be
sparser than chol (S' * S).
p = ccolamd (S, 1) optimizes the ordering for
lu (S(:, p)). The ordering is followed by a column
elimination tree post-ordering.
knobs is an optional 1-element to 5-element input vector, with a
default value of [0 10 10 1 0] if not present or empty. Entries not
present are set to their defaults.
knobs(1)if nonzero, the ordering is optimized for lu (S(:, p)). It will be a
poor ordering for chol (S(:, p)' * S(:, p)).
This is the most important knob for ccolamd.
knobs(2)if S is m-by-n, rows with more than
max (16, knobs(2) * sqrt (n)) entries are ignored.
knobs(3)columns with more than
max (16, knobs(3) * sqrt (min (m, n))) entries are
ignored and ordered last in the output permutation
(subject to the cmember constraints).
knobs(4)if nonzero, aggressive absorption is performed.
knobs(5)if nonzero, statistics and knobs are printed.
cmember is an optional vector of length n. It defines the
constraints on the column ordering. If cmember(j) = c,
then column j is in constraint set c (c must be in the
range 1 to n). In the output permutation p, all columns in set 1
appear first, followed by all columns in set 2, and so on.
cmember = ones (1,n) if not present or empty.
ccolamd (S, [], 1 : n) returns 1 : n
p = ccolamd (S) is about the same as
p = colamd (S). knobs and its default values
differ. colamd always does aggressive absorption, and it finds an
ordering suitable for both lu (S(:, p)) and chol
(S(:, p)' * S(:, p)); it cannot optimize its
ordering for lu (S(:, p)) to the extent that
ccolamd (S, 1) can.
stats is an optional 20-element output vector that provides data
about the ordering and the validity of the input matrix S. Ordering
statistics are in stats(1 : 3). stats(1) and
stats(2) are the number of dense or empty rows and columns
ignored by CCOLAMD and stats(3) is the number of garbage
collections performed on the internal data structure used by CCOLAMD
(roughly of size 2.2 * nnz (S) + 4 * m + 7 * n
integers).
stats(4 : 7) provide information if CCOLAMD was able to
continue. The matrix is OK if stats(4) is zero, or 1 if
invalid. stats(5) is the rightmost column index that is
unsorted or contains duplicate entries, or zero if no such column exists.
stats(6) is the last seen duplicate or out-of-order row
index in the column index given by stats(5), or zero if no
such row index exists. stats(7) is the number of duplicate
or out-of-order row indices. stats(8 : 20) is always zero in
the current version of CCOLAMD (reserved for future use).
The authors of the code itself are S. Larimore, T. Davis and S. Rajamanickam in collaboration with J. Bilbert and E. Ng. Supported by the National Science Foundation (DMS-9504974, DMS-9803599, CCR-0203270), and a grant from Sandia National Lab. See http://faculty.cse.tamu.edu/davis/suitesparse.html for ccolamd, csymamd, amd, colamd, symamd, and other related orderings.
Compute the column approximate minimum degree permutation.
p = colamd (S) returns the column approximate minimum
degree permutation vector for the sparse matrix S. For a
non-symmetric matrix S, S(:,p) tends to have
sparser LU factors than S. The Cholesky factorization of
S(:,p)' * S(:,p) also tends to be sparser
than that of S' * S.
knobs is an optional one- to three-element input vector. If S
is m-by-n, then rows with more than max(16,knobs(1)*sqrt(n))
entries are ignored. Columns with more than
max (16,knobs(2)*sqrt(min(m,n))) entries are removed prior to
ordering, and ordered last in the output permutation p. Only
completely dense rows or columns are removed if knobs(1) and
knobs(2) are < 0, respectively. If knobs(3) is
nonzero, stats and knobs are printed. The default is
knobs = [10 10 0]. Note that knobs differs from earlier
versions of colamd.
stats is an optional 20-element output vector that provides data
about the ordering and the validity of the input matrix S. Ordering
statistics are in stats(1:3). stats(1) and
stats(2) are the number of dense or empty rows and columns
ignored by COLAMD and stats(3) is the number of garbage
collections performed on the internal data structure used by COLAMD
(roughly of size 2.2 * nnz(S) + 4 * m + 7 * n
integers).
Octave built-in functions are intended to generate valid sparse matrices, with no duplicate entries, with ascending row indices of the nonzeros in each column, with a non-negative number of entries in each column (!) and so on. If a matrix is invalid, then COLAMD may or may not be able to continue. If there are duplicate entries (a row index appears two or more times in the same column) or if the row indices in a column are out of order, then COLAMD can correct these errors by ignoring the duplicate entries and sorting each column of its internal copy of the matrix S (the input matrix S is not repaired, however). If a matrix is invalid in other ways then COLAMD cannot continue, an error message is printed, and no output arguments (p or stats) are returned. COLAMD is thus a simple way to check a sparse matrix to see if it’s valid.
stats(4:7) provide information if COLAMD was able to
continue. The matrix is OK if stats(4) is zero, or 1 if
invalid. stats(5) is the rightmost column index that is
unsorted or contains duplicate entries, or zero if no such column exists.
stats(6) is the last seen duplicate or out-of-order row
index in the column index given by stats(5), or zero if no
such row index exists. stats(7) is the number of duplicate
or out-of-order row indices. stats(8:20) is always zero in
the current version of COLAMD (reserved for future use).
The ordering is followed by a column elimination tree post-ordering.
The authors of the code itself are Stefan I. Larimore and Timothy A. Davis. The algorithm was developed in collaboration with John Gilbert, Xerox PARC, and Esmond Ng, Oak Ridge National Laboratory. (see http://faculty.cse.tamu.edu/davis/suitesparse.html)
Return the column permutations such that the columns of
s(:, p) are ordered in terms of increasing number of
nonzero elements.
If s is symmetric, then p is chosen such that
s(p, p) orders the rows and columns with
increasing number of nonzero elements.
For a symmetric positive definite matrix S, return the permutation
vector p such that S(p,p) tends to have a
sparser Cholesky factor than S.
Sometimes csymamd works well for symmetric indefinite matrices too.
The matrix S is assumed to be symmetric; only the strictly lower
triangular part is referenced. S must be square. The ordering is
followed by an elimination tree post-ordering.
knobs is an optional 1-element to 3-element input vector, with a
default value of [10 1 0]. Entries not present are set to their
defaults.
knobs(1)If S is n-by-n, then rows and columns with more than
max(16,knobs(1)*sqrt(n)) entries are ignored, and ordered
last in the output permutation (subject to the cmember constraints).
knobs(2)If nonzero, aggressive absorption is performed.
knobs(3)If nonzero, statistics and knobs are printed.
cmember is an optional vector of length n. It defines the constraints
on the ordering. If cmember(j) = S, then row/column j is
in constraint set c (c must be in the range 1 to n). In the
output permutation p, rows/columns in set 1 appear first, followed
by all rows/columns in set 2, and so on. cmember = ones (1,n)
if not present or empty. csymamd (S,[],1:n) returns
1:n.
p = csymamd (S) is about the same as
p = symamd (S). knobs and its default values
differ.
stats(4:7) provide information if CCOLAMD was able to
continue. The matrix is OK if stats(4) is zero, or 1 if
invalid. stats(5) is the rightmost column index that is
unsorted or contains duplicate entries, or zero if no such column exists.
stats(6) is the last seen duplicate or out-of-order row
index in the column index given by stats(5), or zero if no
such row index exists. stats(7) is the number of duplicate
or out-of-order row indices. stats(8:20) is always zero in
the current version of CCOLAMD (reserved for future use).
The authors of the code itself are S. Larimore, T. Davis and S. Rajamanickam in collaboration with J. Bilbert and E. Ng. Supported by the National Science Foundation (DMS-9504974, DMS-9803599, CCR-0203270), and a grant from Sandia National Lab. See http://faculty.cse.tamu.edu/davis/suitesparse.html for ccolamd, colamd, csymamd, amd, colamd, symamd, and other related orderings.
Perform a Dulmage-Mendelsohn permutation of the sparse matrix S.
With a single output argument dmperm performs the row permutations
p such that S(p,:) has no zero elements on the
diagonal.
Called with two or more output arguments, returns the row and column
permutations, such that S(p, q) is in block
triangular form. The values of r and S define the boundaries
of the blocks. If S is square then r == S.
The method used is described in: A. Pothen & C.-J. Fan. Computing the Block Triangular Form of a Sparse Matrix. ACM Trans. Math. Software, 16(4):303–324, 1990.
For a symmetric positive definite matrix S, returns the permutation
vector p such that S(p, p) tends to have a
sparser Cholesky factor than S.
Sometimes symamd works well for symmetric indefinite matrices too.
The matrix S is assumed to be symmetric; only the strictly lower
triangular part is referenced. S must be square.
knobs is an optional one- to two-element input vector. If S is
n-by-n, then rows and columns with more than
max (16,knobs(1)*sqrt(n)) entries are removed prior to
ordering, and ordered last in the output permutation p. No
rows/columns are removed if knobs(1) < 0. If
knobs(2) is nonzero, stats and knobs are
printed. The default is knobs = [10 0]. Note that
knobs differs from earlier versions of symamd.
stats is an optional 20-element output vector that provides data
about the ordering and the validity of the input matrix S. Ordering
statistics are in stats(1:3).
stats(1) = stats(2) is the number of dense or empty rows
and columns ignored by SYMAMD and stats(3) is the number of
garbage collections performed on the internal data structure used by SYMAMD
(roughly of size 8.4 * nnz (tril (S, -1)) + 9 * n
integers).
Octave built-in functions are intended to generate valid sparse matrices, with no duplicate entries, with ascending row indices of the nonzeros in each column, with a non-negative number of entries in each column (!) and so on. If a matrix is invalid, then SYMAMD may or may not be able to continue. If there are duplicate entries (a row index appears two or more times in the same column) or if the row indices in a column are out of order, then SYMAMD can correct these errors by ignoring the duplicate entries and sorting each column of its internal copy of the matrix S (the input matrix S is not repaired, however). If a matrix is invalid in other ways then SYMAMD cannot continue, an error message is printed, and no output arguments (p or stats) are returned. SYMAMD is thus a simple way to check a sparse matrix to see if it’s valid.
stats(4:7) provide information if SYMAMD was able to
continue. The matrix is OK if stats (4) is zero, or 1
if invalid. stats(5) is the rightmost column index that
is unsorted or contains duplicate entries, or zero if no such column
exists. stats(6) is the last seen duplicate or out-of-order
row index in the column index given by stats(5), or zero
if no such row index exists. stats(7) is the number of
duplicate or out-of-order row indices. stats(8:20) is
always zero in the current version of SYMAMD (reserved for future use).
The ordering is followed by a column elimination tree post-ordering.
The authors of the code itself are Stefan I. Larimore and Timothy A. Davis. The algorithm was developed in collaboration with John Gilbert, Xerox PARC, and Esmond Ng, Oak Ridge National Laboratory. (see http://faculty.cse.tamu.edu/davis/suitesparse.html)
Return the symmetric reverse Cuthill-McKee permutation of S.
p is a permutation vector such that
S(p, p) tends to have its diagonal elements closer
to the diagonal than S. This is a good preordering for LU or
Cholesky factorization of matrices that come from “long, skinny”
problems. It works for both symmetric and asymmetric S.
The algorithm represents a heuristic approach to the NP-complete bandwidth minimization problem. The implementation is based in the descriptions found in
E. Cuthill, J. McKee. Reducing the Bandwidth of Sparse Symmetric Matrices. Proceedings of the 24th ACM National Conference, 157–172 1969, Brandon Press, New Jersey.
A. George, J.W.H. Liu. Computer Solution of Large Sparse Positive Definite Systems, Prentice Hall Series in Computational Mathematics, ISBN 0-13-165274-5, 1981.
Previous: Return Types of Operators and Functions, Up: Operators and Functions [Contents][Index]