Figure 15.5: Mesh plot.
Next: Plot Annotations, Previous: Two-Dimensional Plots, Up: High-Level Plotting [Contents][Index]
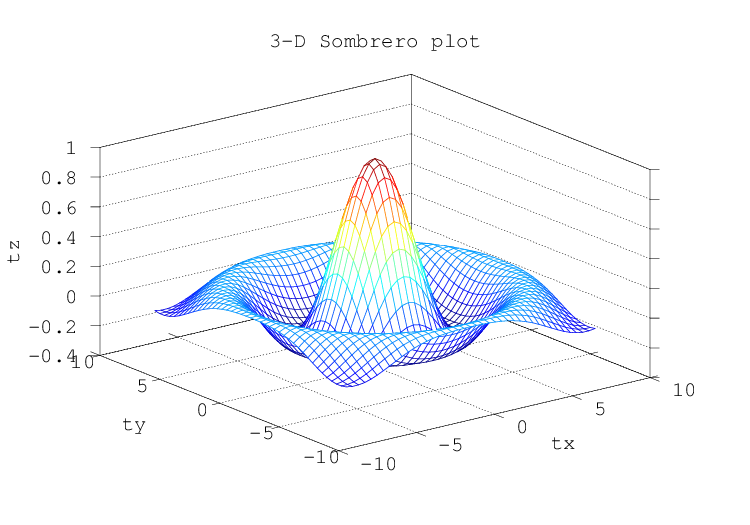
The function mesh produces mesh surface plots. For example,
tx = ty = linspace (-8, 8, 41)'; [xx, yy] = meshgrid (tx, ty); r = sqrt (xx .^ 2 + yy .^ 2) + eps; tz = sin (r) ./ r; mesh (tx, ty, tz);
produces the familiar “sombrero” plot shown in Figure 15.5. Note
the use of the function meshgrid to create matrices of X and Y
coordinates to use for plotting the Z data. The ndgrid function
is similar to meshgrid, but works for N-dimensional matrices.
The meshc function is similar to mesh, but also produces a
plot of contours for the surface.
The plot3 function displays arbitrary three-dimensional data,
without requiring it to form a surface. For example,
t = 0:0.1:10*pi; r = linspace (0, 1, numel (t)); z = linspace (0, 1, numel (t)); plot3 (r.*sin(t), r.*cos(t), z);
displays the spiral in three dimensions shown in Figure 15.6.
Finally, the view function changes the viewpoint for
three-dimensional plots.
Plot a 3-D wireframe mesh.
The wireframe mesh is plotted using rectangles. The vertices of the
rectangles [x, y] are typically the output of meshgrid.
over a 2-D rectangular region in the x-y plane. z determines the
height above the plane of each vertex. If only a single z matrix is
given, then it is plotted over the meshgrid
x = 1:columns (z), y = 1:rows (z).
Thus, columns of z correspond to different x values and rows
of z correspond to different y values.
The color of the mesh is computed by linearly scaling the z values
to fit the range of the current colormap. Use caxis and/or
change the colormap to control the appearance.
Optionally, the color of the mesh can be specified independently of z by supplying a color matrix, c.
Any property/value pairs are passed directly to the underlying surface object.
If the first argument hax is an axes handle, then plot into this axis,
rather than the current axes returned by gca.
The optional return value h is a graphics handle to the created surface object.
See also: ezmesh, meshc, meshz, trimesh, contour, surf, surface, meshgrid, hidden, shading, colormap, caxis.
Plot a 3-D wireframe mesh with underlying contour lines.
The wireframe mesh is plotted using rectangles. The vertices of the
rectangles [x, y] are typically the output of meshgrid.
over a 2-D rectangular region in the x-y plane. z determines the
height above the plane of each vertex. If only a single z matrix is
given, then it is plotted over the meshgrid
x = 1:columns (z), y = 1:rows (z).
Thus, columns of z correspond to different x values and rows
of z correspond to different y values.
The color of the mesh is computed by linearly scaling the z values
to fit the range of the current colormap. Use caxis and/or
change the colormap to control the appearance.
Optionally the color of the mesh can be specified independently of z by supplying a color matrix, c.
Any property/value pairs are passed directly to the underlying surface object.
If the first argument hax is an axes handle, then plot into this axis,
rather than the current axes returned by gca.
The optional return value h is a 2-element vector with a graphics handle to the created surface object and to the created contour plot.
See also: ezmeshc, mesh, meshz, contour, surfc, surface, meshgrid, hidden, shading, colormap, caxis.
Plot a 3-D wireframe mesh with a surrounding curtain.
The wireframe mesh is plotted using rectangles. The vertices of the
rectangles [x, y] are typically the output of meshgrid.
over a 2-D rectangular region in the x-y plane. z determines the
height above the plane of each vertex. If only a single z matrix is
given, then it is plotted over the meshgrid
x = 0:columns (z) - 1, y = 0:rows (z) - 1.
Thus, columns of z correspond to different x values and rows
of z correspond to different y values.
The color of the mesh is computed by linearly scaling the z values
to fit the range of the current colormap. Use caxis and/or
change the colormap to control the appearance.
Optionally the color of the mesh can be specified independently of z by supplying a color matrix, c.
Any property/value pairs are passed directly to the underlying surface object.
If the first argument hax is an axes handle, then plot into this axis,
rather than the current axes returned by gca.
The optional return value h is a graphics handle to the created surface object.
See also: mesh, meshc, contour, surf, surface, waterfall, meshgrid, hidden, shading, colormap, caxis.
Control mesh hidden line removal.
When called with no argument the hidden line removal state is toggled.
When called with one of the modes "on" or "off" the state
is set accordingly.
The optional output argument mode is the current state.
Hidden Line Removal determines what graphic objects behind a mesh plot are visible. The default is for the mesh to be opaque and lines behind the mesh are not visible. If hidden line removal is turned off then objects behind the mesh can be seen through the faces (openings) of the mesh, although the mesh grid lines are still opaque.
See also: mesh, meshc, meshz, ezmesh, ezmeshc, trimesh, waterfall.
Plot a 3-D surface mesh.
The surface mesh is plotted using shaded rectangles. The vertices of the
rectangles [x, y] are typically the output of meshgrid.
over a 2-D rectangular region in the x-y plane. z determines the
height above the plane of each vertex. If only a single z matrix is
given, then it is plotted over the meshgrid
x = 1:columns (z), y = 1:rows (z).
Thus, columns of z correspond to different x values and rows
of z correspond to different y values.
The color of the surface is computed by linearly scaling the z values
to fit the range of the current colormap. Use caxis and/or
change the colormap to control the appearance.
Optionally, the color of the surface can be specified independently of z by supplying a color matrix, c.
Any property/value pairs are passed directly to the underlying surface object.
If the first argument hax is an axes handle, then plot into this axis,
rather than the current axes returned by gca.
The optional return value h is a graphics handle to the created surface object.
Note: The exact appearance of the surface can be controlled with the
shading command or by using set to control surface object
properties.
See also: ezsurf, surfc, surfl, surfnorm, trisurf, contour, mesh, surface, meshgrid, hidden, shading, colormap, caxis.
Plot a 3-D surface mesh with underlying contour lines.
The surface mesh is plotted using shaded rectangles. The vertices of the
rectangles [x, y] are typically the output of meshgrid.
over a 2-D rectangular region in the x-y plane. z determines the
height above the plane of each vertex. If only a single z matrix is
given, then it is plotted over the meshgrid
x = 1:columns (z), y = 1:rows (z).
Thus, columns of z correspond to different x values and rows
of z correspond to different y values.
The color of the surface is computed by linearly scaling the z values
to fit the range of the current colormap. Use caxis and/or
change the colormap to control the appearance.
Optionally, the color of the surface can be specified independently of z by supplying a color matrix, c.
Any property/value pairs are passed directly to the underlying surface object.
If the first argument hax is an axes handle, then plot into this axis,
rather than the current axes returned by gca.
The optional return value h is a graphics handle to the created surface object.
Note: The exact appearance of the surface can be controlled with the
shading command or by using set to control surface object
properties.
See also: ezsurfc, surf, surfl, surfnorm, trisurf, contour, mesh, surface, meshgrid, hidden, shading, colormap, caxis.
Plot a 3-D surface using shading based on various lighting models.
The surface mesh is plotted using shaded rectangles. The vertices of the
rectangles [x, y] are typically the output of meshgrid.
over a 2-D rectangular region in the x-y plane. z determines the
height above the plane of each vertex. If only a single z matrix is
given, then it is plotted over the meshgrid
x = 1:columns (z), y = 1:rows (z).
Thus, columns of z correspond to different x values and rows
of z correspond to different y values.
The default lighting mode "cdata", changes the cdata property of the
surface object to give the impression of a lighted surface.
Warning: The alternative mode "light" mode which creates a
light object to illuminate the surface is not implemented (yet).
The light source location can be specified using lsrc. It can be given as a 2-element vector [azimuth, elevation] in degrees, or as a 3-element vector [lx, ly, lz]. The default value is rotated 45 degrees counterclockwise to the current view.
The material properties of the surface can specified using a 4-element vector P = [AM D SP exp] which defaults to p = [0.55 0.6 0.4 10].
"AM" strength of ambient light"D" strength of diffuse reflection"SP" strength of specular reflection"EXP" specular exponentIf the first argument hax is an axes handle, then plot into this axis,
rather than the current axes returned by gca.
The optional return value h is a graphics handle to the created surface object.
Example:
colormap (bone (64)); surfl (peaks); shading interp;
See also: diffuse, specular, surf, shading, colormap, caxis.
Find the vectors normal to a meshgridded surface.
If x and y are vectors, then a typical vertex is
(x(j), y(i), z(i,j)). Thus, columns of z correspond
to different x values and rows of z correspond to different
y values. If only a single input z is given then x is
taken to be 1:rows (z) and y is
1:columns (z).
If no return arguments are requested, a surface plot with the normal vectors to the surface is plotted.
Any property/value input pairs are assigned to the surface object.
If the first argument hax is an axes handle, then plot into this axis,
rather than the current axes returned by gca.
If output arguments are requested then the components of the normal vectors are returned in nx, ny, and nz and no plot is made.
An example of the use of surfnorm is
surfnorm (peaks (25));
Algorithm: The normal vectors are calculated by taking the cross product of the diagonals of each of the quadrilaterals in the meshgrid to find the normal vectors of the centers of these quadrilaterals. The four nearest normal vectors to the meshgrid points are then averaged to obtain the normal to the surface at the meshgridded points.
See also: isonormals, quiver3, surf, meshgrid.
Calculate isosurface of 3-D data.
If called with one output argument and the first input argument
val is a three-dimensional array that contains the data of an
isosurface geometry and the second input argument iso keeps the
isovalue as a scalar value then return a structure array fv
that contains the fields Faces and Vertices at computed
points [x, y, z] = meshgrid (1:l, 1:m, 1:n). The output
argument fv can directly be taken as an input argument for the
patch function.
If called with further input arguments x, y and z which are three–dimensional arrays with the same size than val then the volume data is taken at those given points.
The string input argument "noshare" is only for compatibility and
has no effect. If given the string input argument
"verbose" then print messages to the command line interface about the
current progress.
If called with the input argument col which is a three-dimensional array of the same size than val then take those values for the interpolation of coloring the isosurface geometry. Add the field FaceVertexCData to the structure array fv.
If called with two or three output arguments then return the information about the faces f, vertices v and color data c as separate arrays instead of a single structure array.
If called with no output argument then directly process the
isosurface geometry with the patch command.
For example,
[x, y, z] = meshgrid (1:5, 1:5, 1:5); val = rand (5, 5, 5); isosurface (x, y, z, val, .5);
will directly draw a random isosurface geometry in a graphics window. Another example for an isosurface geometry with different additional coloring
N = 15; # Increase number of vertices in each direction
iso = .4; # Change isovalue to .1 to display a sphere
lin = linspace (0, 2, N);
[x, y, z] = meshgrid (lin, lin, lin);
c = abs ((x-.5).^2 + (y-.5).^2 + (z-.5).^2);
figure (); # Open another figure window
subplot (2,2,1); view (-38, 20);
[f, v] = isosurface (x, y, z, c, iso);
p = patch ("Faces", f, "Vertices", v, "EdgeColor", "none");
set (gca, "PlotBoxAspectRatioMode", "manual", ...
"PlotBoxAspectRatio", [1 1 1]);
# set (p, "FaceColor", "green", "FaceLighting", "phong");
# light ("Position", [1 1 5]); # Available with the JHandles package
subplot (2,2,2); view (-38, 20);
p = patch ("Faces", f, "Vertices", v, "EdgeColor", "blue");
set (gca, "PlotBoxAspectRatioMode", "manual", ...
"PlotBoxAspectRatio", [1 1 1]);
# set (p, "FaceColor", "none", "FaceLighting", "phong");
# light ("Position", [1 1 5]);
subplot (2,2,3); view (-38, 20);
[f, v, c] = isosurface (x, y, z, c, iso, y);
p = patch ("Faces", f, "Vertices", v, "FaceVertexCData", c, ...
"FaceColor", "interp", "EdgeColor", "none");
set (gca, "PlotBoxAspectRatioMode", "manual", ...
"PlotBoxAspectRatio", [1 1 1]);
# set (p, "FaceLighting", "phong");
# light ("Position", [1 1 5]);
subplot (2,2,4); view (-38, 20);
p = patch ("Faces", f, "Vertices", v, "FaceVertexCData", c, ...
"FaceColor", "interp", "EdgeColor", "blue");
set (gca, "PlotBoxAspectRatioMode", "manual", ...
"PlotBoxAspectRatio", [1 1 1]);
# set (p, "FaceLighting", "phong");
# light ("Position", [1 1 5]);
See also: isonormals, isocolors.
Calculate normals to an isosurface.
If called with one output argument and the first input argument
val is a three-dimensional array that contains the data for an
isosurface geometry and the second input argument v keeps the
vertices of an isosurface then return the normals n in form of
a matrix with the same size than v at computed points
[x, y, z] = meshgrid (1:l, 1:m, 1:n). The output argument
n can be taken to manually set VertexNormals of a patch.
If called with further input arguments x, y and z which are three–dimensional arrays with the same size than val then the volume data is taken at those given points. Instead of the vertices data v a patch handle p can be passed to this function.
If given the string input argument "negate" as last input argument
then compute the reverse vector normals of an isosurface geometry.
If no output argument is given then directly redraw the patch that is given by the patch handle p.
For example:
function [] = isofinish (p)
set (gca, "PlotBoxAspectRatioMode", "manual", ...
"PlotBoxAspectRatio", [1 1 1]);
set (p, "VertexNormals", -get (p,"VertexNormals")); # Revert normals
set (p, "FaceColor", "interp");
## set (p, "FaceLighting", "phong");
## light ("Position", [1 1 5]); # Available with JHandles
endfunction
N = 15; # Increase number of vertices in each direction
iso = .4; # Change isovalue to .1 to display a sphere
lin = linspace (0, 2, N);
[x, y, z] = meshgrid (lin, lin, lin);
c = abs ((x-.5).^2 + (y-.5).^2 + (z-.5).^2);
figure (); # Open another figure window
subplot (2,2,1); view (-38, 20);
[f, v, cdat] = isosurface (x, y, z, c, iso, y);
p = patch ("Faces", f, "Vertices", v, "FaceVertexCData", cdat, ...
"FaceColor", "interp", "EdgeColor", "none");
isofinish (p); # Call user function isofinish
subplot (2,2,2); view (-38, 20);
p = patch ("Faces", f, "Vertices", v, "FaceVertexCData", cdat, ...
"FaceColor", "interp", "EdgeColor", "none");
isonormals (x, y, z, c, p); # Directly modify patch
isofinish (p);
subplot (2,2,3); view (-38, 20);
p = patch ("Faces", f, "Vertices", v, "FaceVertexCData", cdat, ...
"FaceColor", "interp", "EdgeColor", "none");
n = isonormals (x, y, z, c, v); # Compute normals of isosurface
set (p, "VertexNormals", n); # Manually set vertex normals
isofinish (p);
subplot (2,2,4); view (-38, 20);
p = patch ("Faces", f, "Vertices", v, "FaceVertexCData", cdat, ...
"FaceColor", "interp", "EdgeColor", "none");
isonormals (x, y, z, c, v, "negate"); # Use reverse directly
isofinish (p);
See also: isosurface, isocolors.
Compute isosurface colors.
If called with one output argument and the first input argument
c is a three-dimensional array that contains color values and
the second input argument v keeps the vertices of a geometry
then return a matrix cd with color data information for the
geometry at computed points
[x, y, z] = meshgrid (1:l, 1:m, 1:n). The output argument
cd can be taken to manually set FaceVertexCData of a patch.
If called with further input arguments x, y and z
which are three–dimensional arrays of the same size than c
then the color data is taken at those given points. Instead of the
color data c this function can also be called with RGB values
r, g, b. If input argumnets x, y,
z are not given then again meshgrid computed values
are taken.
Optionally, the patch handle p can be given as the last input argument to all variations of function calls instead of the vertices data v. Finally, if no output argument is given then directly change the colors of a patch that is given by the patch handle p.
For example:
function [] = isofinish (p)
set (gca, "PlotBoxAspectRatioMode", "manual", ...
"PlotBoxAspectRatio", [1 1 1]);
set (p, "FaceColor", "interp");
## set (p, "FaceLighting", "flat");
## light ("Position", [1 1 5]); # Available with JHandles
endfunction
N = 15; # Increase number of vertices in each direction
iso = .4; # Change isovalue to .1 to display a sphere
lin = linspace (0, 2, N);
[x, y, z] = meshgrid (lin, lin, lin);
c = abs ((x-.5).^2 + (y-.5).^2 + (z-.5).^2);
figure (); # Open another figure window
subplot (2,2,1); view (-38, 20);
[f, v] = isosurface (x, y, z, c, iso);
p = patch ("Faces", f, "Vertices", v, "EdgeColor", "none");
cdat = rand (size (c)); # Compute random patch color data
isocolors (x, y, z, cdat, p); # Directly set colors of patch
isofinish (p); # Call user function isofinish
subplot (2,2,2); view (-38, 20);
p = patch ("Faces", f, "Vertices", v, "EdgeColor", "none");
[r, g, b] = meshgrid (lin, 2-lin, 2-lin);
cdat = isocolors (x, y, z, c, v); # Compute color data vertices
set (p, "FaceVertexCData", cdat); # Set color data manually
isofinish (p);
subplot (2,2,3); view (-38, 20);
p = patch ("Faces", f, "Vertices", v, "EdgeColor", "none");
cdat = isocolors (r, g, b, c, p); # Compute color data patch
set (p, "FaceVertexCData", cdat); # Set color data manually
isofinish (p);
subplot (2,2,4); view (-38, 20);
p = patch ("Faces", f, "Vertices", v, "EdgeColor", "none");
r = g = b = repmat ([1:N] / N, [N, 1, N]); # Black to white
cdat = isocolors (x, y, z, r, g, b, v);
set (p, "FaceVertexCData", cdat);
isofinish (p);
See also: isosurface, isonormals.
Reduce the size of faces in a patch by the shrink factor sf.
The patch object can be specified by a graphics handle (p), a patch
structure (fv) with the fields "faces" and "vertices",
or as two separate matrices (f, v) of faces and vertices.
The shrink factor sf is a positive number specifying the percentage of the original area the new face will occupy. If no factor is given the default is 0.3 (a reduction to 30% of the original size). A factor greater than 1.0 will result in the expansion of faces.
Given a patch handle as the first input argument and no output parameters, perform the shrinking of the patch faces in place and redraw the patch.
If called with one output argument, return a structure with fields
"faces", "vertices", and "facevertexcdata"
containing the data after shrinking. This structure can be used directly
as an input argument to the patch function.
Caution:: Performing the shrink operation on faces which are not convex can lead to undesirable results.
Example: a triangulated 3/4 circle and the corresponding shrunken version.
[phi r] = meshgrid (linspace (0, 1.5*pi, 16), linspace (1, 2, 4));
tri = delaunay (phi(:), r(:));
v = [r(:).*sin(phi(:)) r(:).*cos(phi(:))];
clf ()
p = patch ("Faces", tri, "Vertices", v, "FaceColor", "none");
fv = shrinkfaces (p);
patch (fv)
axis equal
grid on
See also: patch.
Calculate the diffuse reflection strength of a surface defined by the normal vector elements sx, sy, sz.
The light source location vector lv can be given as a 2-element vector [azimuth, elevation] in degrees or as a 3-element vector [x, y, z].
Calculate the specular reflection strength of a surface defined by the normal vector elements sx, sy, sz using Phong’s approximation.
The light source location and viewer location vectors are specified using parameters lv and vv respectively. The location vectors can given as 2-element vectors [azimuth, elevation] in degrees or as 3-element vectors [x, y, z].
An optional sixth argument specifies the specular exponent (spread) se. If not given, se defaults to 10.
Given vectors of x and y coordinates, return matrices xx and yy corresponding to a full 2-D grid.
The rows of xx are copies of x, and the columns of yy are copies of y. If y is omitted, then it is assumed to be the same as x.
If the optional z input is given, or zz is requested, then the output will be a full 3-D grid.
meshgrid is most frequently used to produce input for a 2-D or 3-D
function that will be plotted. The following example creates a surface
plot of the “sombrero” function.
f = @(x,y) sin (sqrt (x.^2 + y.^2)) ./ sqrt (x.^2 + y.^2); range = linspace (-8, 8, 41); [X, Y] = meshgrid (range, range); Z = f (X, Y); surf (X, Y, Z);
Programming Note: meshgrid is restricted to 2-D or 3-D grid
generation. The ndgrid function will generate 1-D through N-D
grids. However, the functions are not completely equivalent. If x
is a vector of length M and y is a vector of length N, then
meshgrid will produce an output grid which is NxM. ndgrid
will produce an output which is MxN (transpose) for the same
input. Some core functions expect meshgrid input and others expect
ndgrid input. Check the documentation for the function in question
to determine the proper input format.
Given n vectors x1, …, xn, ndgrid returns n
arrays of dimension n.
The elements of the i-th output argument contains the elements of the vector xi repeated over all dimensions different from the i-th dimension. Calling ndgrid with only one input argument x is equivalent to calling ndgrid with all n input arguments equal to x:
[y1, y2, …, yn] = ndgrid (x, …, x)
Programming Note: ndgrid is very similar to the function
meshgrid except that the first two dimensions are transposed in
comparison to meshgrid. Some core functions expect meshgrid
input and others expect ndgrid input. Check the documentation for
the function in question to determine the proper input format.
See also: meshgrid.
Produce 3-D plots.
Many different combinations of arguments are possible. The simplest form is
plot3 (x, y, z)
in which the arguments are taken to be the vertices of the points to be plotted in three dimensions. If all arguments are vectors of the same length, then a single continuous line is drawn. If all arguments are matrices, then each column of is treated as a separate line. No attempt is made to transpose the arguments to make the number of rows match.
If only two arguments are given, as
plot3 (x, cplx)
the real and imaginary parts of the second argument are used as the y and z coordinates, respectively.
If only one argument is given, as
plot3 (cplx)
the real and imaginary parts of the argument are used as the y and z values, and they are plotted versus their index.
Arguments may also be given in groups of three as
plot3 (x1, y1, z1, x2, y2, z2, …)
in which each set of three arguments is treated as a separate line or set of lines in three dimensions.
To plot multiple one- or two-argument groups, separate each group with an empty format string, as
plot3 (x1, c1, "", c2, "", …)
Multiple property-value pairs may be specified which will affect the line
objects drawn by plot3. If the fmt argument is supplied it
will format the line objects in the same manner as plot.
If the first argument hax is an axes handle, then plot into this axis,
rather than the current axes returned by gca.
The optional return value h is a graphics handle to the created plot.
Example:
z = [0:0.05:5]; plot3 (cos (2*pi*z), sin (2*pi*z), z, ";helix;"); plot3 (z, exp (2i*pi*z), ";complex sinusoid;");
Query or set the viewpoint for the current axes.
The parameters azimuth and elevation can be given as two arguments or as 2-element vector. The viewpoint can also be specified with Cartesian coordinates x, y, and z.
The call view (2) sets the viewpoint to azimuth = 0
and elevation = 90, which is the default for 2-D graphs.
The call view (3) sets the viewpoint to azimuth = -37.5
and elevation = 30, which is the default for 3-D graphs.
If the first argument hax is an axes handle, then operate on
this axis rather than the current axes returned by gca.
If no inputs are given, return the current azimuth and elevation.
Plot slices of 3-D data/scalar fields.
Each element of the 3-dimensional array v represents a scalar value at
a location given by the parameters x, y, and z. The
parameters x, x, and z are either 3-dimensional arrays of
the same size as the array v in the "meshgrid" format or
vectors. The parameters xi, etc. respect a similar format to
x, etc., and they represent the points at which the array vi
is interpolated using interp3. The vectors sx, sy, and
sz contain points of orthogonal slices of the respective axes.
If x, y, z are omitted, they are assumed to be
x = 1:size (v, 2), y = 1:size (v, 1) and
z = 1:size (v, 3).
method is one of:
"nearest"Return the nearest neighbor.
"linear"Linear interpolation from nearest neighbors.
"cubic"Cubic interpolation from four nearest neighbors (not implemented yet).
"spline"Cubic spline interpolation—smooth first and second derivatives throughout the curve.
The default method is "linear".
If the first argument hax is an axes handle, then plot into this axis,
rather than the current axes returned by gca.
The optional return value h is a graphics handle to the created surface object.
Examples:
[x, y, z] = meshgrid (linspace (-8, 8, 32)); v = sin (sqrt (x.^2 + y.^2 + z.^2)) ./ (sqrt (x.^2 + y.^2 + z.^2)); slice (x, y, z, v, [], 0, []); [xi, yi] = meshgrid (linspace (-7, 7)); zi = xi + yi; slice (x, y, z, v, xi, yi, zi);
Draw a ribbon plot for the columns of y vs. x.
The optional parameter width specifies the width of a single ribbon
(default is 0.75). If x is omitted, a vector containing the
row numbers is assumed (1:rows (Y)).
If the first argument hax is an axes handle, then plot into this axis,
rather than the current axes returned by gca.
The optional return value h is a vector of graphics handles to the surface objects representing each ribbon.
Set the shading of patch or surface graphic objects.
Valid arguments for type are
"flat"Single colored patches with invisible edges.
"faceted"Single colored patches with visible edges.
"interp"Color between patch vertices are interpolated and the patch edges are invisible.
If the first argument hax is an axes handle, then plot into this axis,
rather than the current axes returned by gca.
Draw a 3-D scatter plot.
A marker is plotted at each point defined by the coordinates in the vectors x, y, and z.
The size of the markers is determined by s, which can be a scalar or a vector of the same length as x, y, and z. If s is not given, or is an empty matrix, then a default value of 8 points is used.
The color of the markers is determined by c, which can be a string defining a fixed color; a 3-element vector giving the red, green, and blue components of the color; a vector of the same length as x that gives a scaled index into the current colormap; or an Nx3 matrix defining the RGB color of each marker individually.
The marker to use can be changed with the style argument, that is a
string defining a marker in the same manner as the plot command.
If no marker is specified it defaults to "o" or circles.
If the argument "filled" is given then the markers are filled.
Additional property/value pairs are passed directly to the underlying patch object.
If the first argument hax is an axes handle, then plot into this axis,
rather than the current axes returned by gca.
The optional return value h is a graphics handle to the hggroup object representing the points.
[x, y, z] = peaks (20); scatter3 (x(:), y(:), z(:), [], z(:));
Plot a 3-D waterfall plot.
A waterfall plot is similar to a meshz plot except only
mesh lines for the rows of z (x-values) are shown.
The wireframe mesh is plotted using rectangles. The vertices of the
rectangles [x, y] are typically the output of meshgrid.
over a 2-D rectangular region in the x-y plane. z determines the
height above the plane of each vertex. If only a single z matrix is
given, then it is plotted over the meshgrid
x = 1:columns (z), y = 1:rows (z).
Thus, columns of z correspond to different x values and rows
of z correspond to different y values.
The color of the mesh is computed by linearly scaling the z values
to fit the range of the current colormap. Use caxis and/or
change the colormap to control the appearance.
Optionally the color of the mesh can be specified independently of z by supplying a color matrix, c.
Any property/value pairs are passed directly to the underlying surface object.
If the first argument hax is an axes handle, then plot into this axis,
rather than the current axes returned by gca.
The optional return value h is a graphics handle to the created surface object.
See also: meshz, mesh, meshc, contour, surf, surface, ribbon, meshgrid, hidden, shading, colormap, caxis.
| • Aspect Ratio: | ||
| • Three-dimensional Function Plotting: | ||
| • Three-dimensional Geometric Shapes: |
Next: Plot Annotations, Previous: Two-Dimensional Plots, Up: High-Level Plotting [Contents][Index]